Can sinXyXy Be Made Continuous at 00
Get the answer to your homework problem.
Try Numerade free for 7 days
University of Wisconsin - Milwaukee
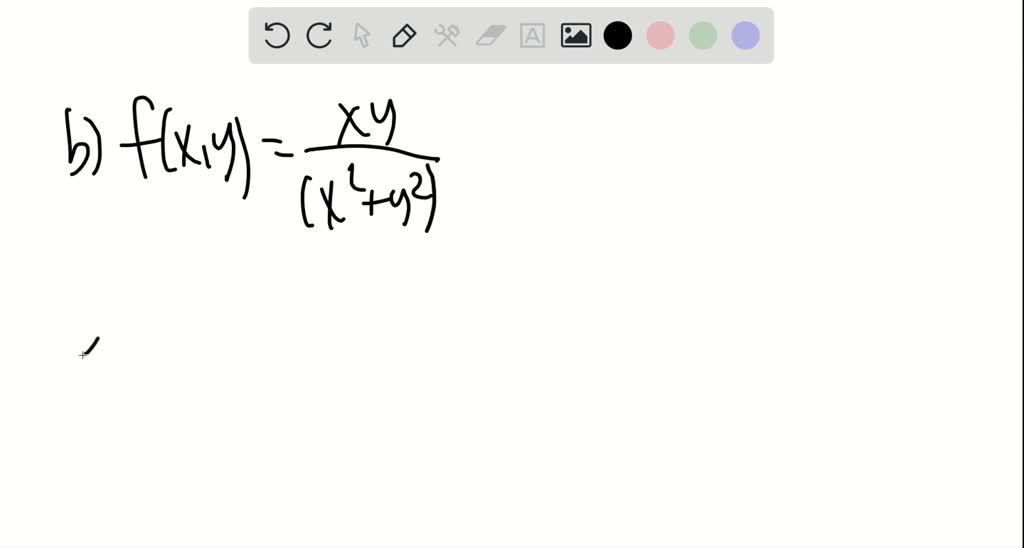
(a) Can $[\sin (x+y)] /(x+y)$ be made continuous by suitably defining it at (0,0)$?$ (b) $\operatorname{Can} x y /\left(x^{2}+y^{2}\right)$ be made continuous by suitably defining it at (0,0)$?$ (c) Prove that $f: \mathbb{R}^{2} \rightarrow \mathbb{R},(x, y) \mapsto y e^{x}+\sin x+(x y)^{4}$ is continuous.
Related Question
(a) Can $[\sin (x+y)] /(x+y)$ be made continuous by suitably defining it at (0,0)$?$ (b) $\operatorname{Can} x y /\left(x^{2}+y^{2}\right)$ be made continuous by suitably defining it at (0,0)$?$ (c) Prove that $f: \mathbb{R}^{2} \rightarrow \mathbb{R},(x, y) \mapsto y e^{x}+\sin x+(x y)^{4}$ is continuous.
Discussion
You must be signed in to discuss.
Video Transcript
Okay, so the function we have here a part A is F of X is equal to sine of X plus Y over X plus Y. Now we know the function F is continuous at X is equal to A If and only if we have the limit as X approaches A. Of F of X is equal to F. Of A. So here we observe that as X Y approaches 00 the expression X plus Y must approach to zero. So let's let X plus Y be equally tea. So let X plus Y the equal to T. And then we have well um clearly we then had the T approaches zero. So we have the limit as X Y um approaches 00 just becomes the limit as T approaches zero of instead of sine of X. Y over X plus Y, we just have signs of T over T. And we know the limit here is equal to one. So therefore the original function um this is going to be equal to one And therefore the function is continuous at 00. By defining f of 0, 0, be equal to one. Okay? And then for part B we consider the expression F of X, Y is equal to x, Y divided by x squared plus Y squared. Ok, so um here we find the limits of F along first the path Y is equal to uh M X. So we have here the limit as X Y approaches 00 of x times M X over X squared plus M X squared, gives us just the limit as X approaches zero of em X squared over X squared plus um square times X squared, which is just equal to M over one plus M squared. And since here M varies in different paths. The limit values. The function are different in different paths. For example, along the path, Y is equal to x. Um We get the limit is equal to one half and along the path Y is equal to zero. Um We get the limits equal to zero. Therefore the limit as X Y approaches 00 of F. Of x, Y does not exist. And um last lethal part C. We have the function F mapping are square to our where we have X. Y maps to Y times E. To the X plus sine of X plus X. Y to the fourth. Okay so the function here is some of three functions and now it's gonna be sufficient to show that each term is confession is um is continuous. Now since we have at the limit as X Y approaches, sign of acts is eager to sign of A. Um And also X. Y to the fourth is a polynomial of two variables is continuous at all points. Um Therefore our function here is going to be continuous.
mcdonaldhicaltisee.blogspot.com
Source: https://www.numerade.com/ask/question/a-can-sin-xy-xy-be-made-continuous-by-suitably-defining-it-at-00-b-operatornamecan-x-y-leftx2y2right-84764/
0 Response to "Can sinXyXy Be Made Continuous at 00"
Publicar un comentario